周胤呈
结构稳定是保证结构安全的重要内容。本篇以混凝土结构为例,来梳理一下规范相关条文以及YJK程序中的实现。
注:本篇除弹性水平位移推导参考徐培福的《复杂高层建筑结构设计》,其余均为个人理解、自行推导。
整体稳定
结构在水平荷载作用下,会发生侧向变形,重力产生二阶效应。分为三个阶段:重力二阶效应较小,可以忽略,不考虑其对结构的影响;重力二阶效应较大,需要考虑其对结构的影响;重力二阶效应很大,需要校核结构是否满足整体稳定的要求。根据《高规》5.4节: 

我们将规范公式用一个简单的图形进行表达:
非框架结构:

框架结构:

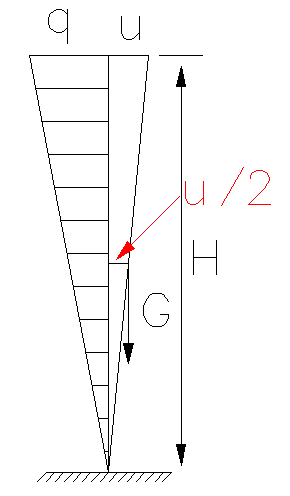
可以看到规范对框架结构、非框架结构“刚重比”的限值不同。这是由于两者在水平力作用下呈现出不同的变形特点,非框架结构往往较高、偏柔,变形呈现“弯曲”或“弯剪”状态,此时进行稳定验算可近似等效为竖向悬臂受弯构件,“刚重比”只需验算整体结构即可;框架结构往往较矮、偏刚,变形呈现出“剪切”状态,“刚重比”需要逐层进行验算。
弯曲型、弯剪型结构
将高度为H的结构等效为竖向悬臂受弯构件,将水平荷载等效为倒三角形分布荷载:
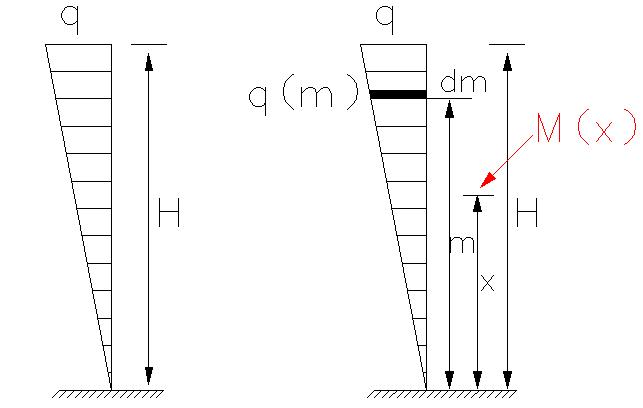
取微元体dm,此处荷载q(m)=mq/H,(m)=q(m).dm,微元对x处弯矩为:F(m)=q(m).dm。
积分得到x处弯矩:
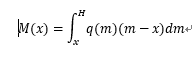
化简后:
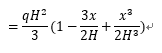
根据《建筑结构静力计算实用手册》荷载作用下弹性位移:
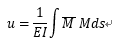

化简后可得:
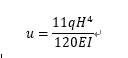
(推导详细可参见徐培福《复杂高层建筑结构设计》)程序计算刚重比采用等效侧向刚度,按倒三角形分布荷载作用下结构顶点位移相等的原则。
根据上述推导可得等效侧向刚度:
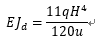
对应《高规》5.4.1条文说明:

《高规》5.4条文说明,结构按弹性分析的二阶效应对结构内力、位移增量控制在5%左右;考虑实际刚度折减50%时,结构内力增量控制在10%以内,重力二阶效应影响较小,可忽略不计。据此进行推导:
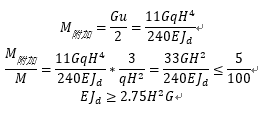
和规范2.7基本相等。即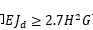 可不考虑重力二阶效应的影响。
可不考虑重力二阶效应的影响。
当重力二阶效应,引起的附加弯矩小于10%时,可以不考虑二阶效应对结构整体稳定性的影响:
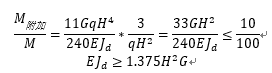
和规范1.4基本相等。即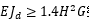 结构整体稳定性满足要求。
结构整体稳定性满足要求。
以一个层高均为6m、6层(含1层地下室)的剪力墙结构模型,手算地震作用下的刚重比(YJK对于刚重比的计算不考虑地下室):

G=5x(1.2x4629+1.4x648)=32310kN。
确定位移时,需要勾选上:

刚重比的计算,程序取质心的位移。由于程序未直接输出质心处的位移,手动复核可以选择离质心最近的节点近似计算。为了更准确的还原计算过程,将对称模型中部布置交叉梁,实现质心在节点上。
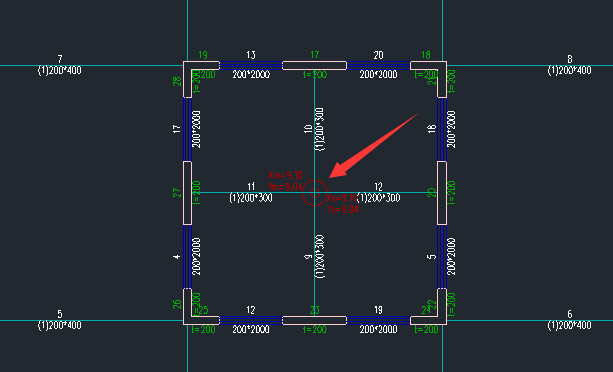
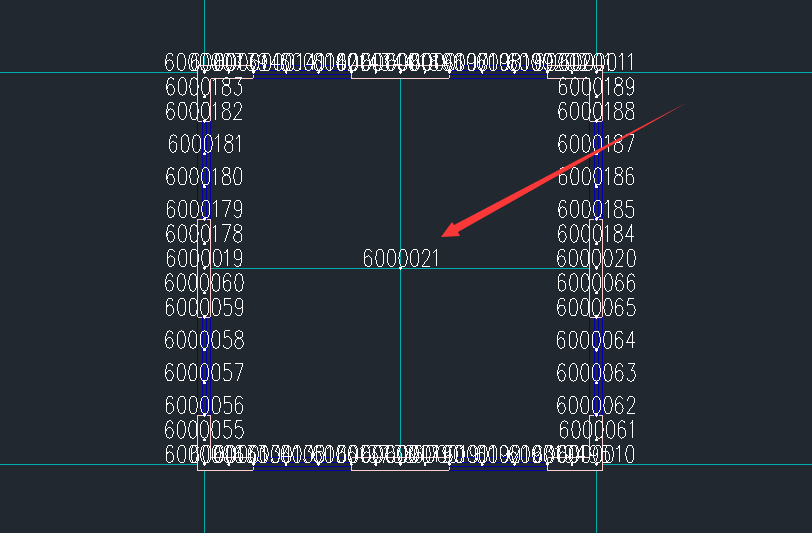
wdisp.out文本中找到对应节点X向地震的顶点位移和地下室底板位移(需扣除地下室部分)


u=6.206-0.124=6.082

剪力取地下室顶板剪力V=1524.27kN
V=qH/2
q=2V/H=2x1524.27/(5x6)=101.618kN/m
EJd=11x101.618x304/(120x6.082x10-3)=1.24x109kN/m
刚重比:EJd/H2G=1.24x109/302x32310=42.64
手核结果和程序输出基本一致:

剪切型
对于剪切型结构,如典型的框架结构,则需要验算每一层的刚重比。框架结构在水平剪力作用下变形如下图:
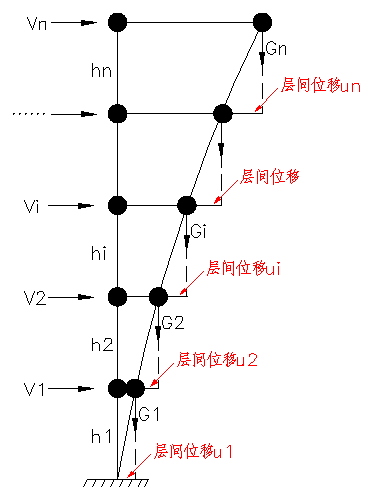
以第i层为例:
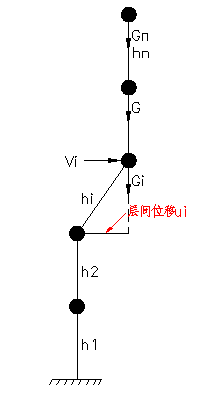
剪切型结构i层受到剪力vi,层间产生ui的变形,层高为hi。
则有:
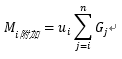
当附加弯矩小于初始弯矩5%时:
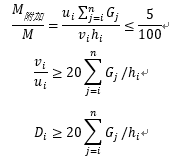
即刚重比大于20时,可不考虑结构的二阶效应。
当附加弯矩小于初始弯矩10%时:
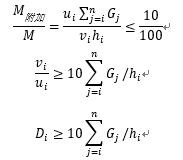
即刚重比大于10时,结构稳定性满足要求。
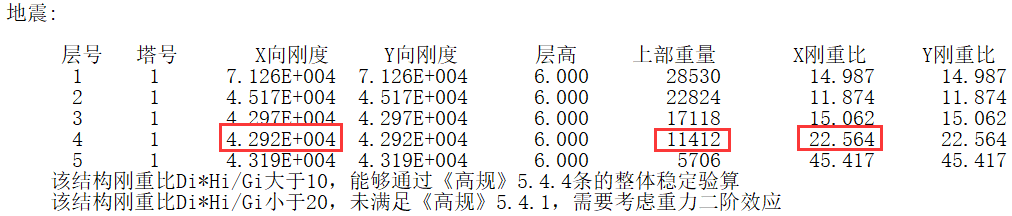
以一个层高均为6m、5层的框架结构模型,来还原一下地震作用下第4层“刚重比”的计算:

u4为第4层质心处的层间位移,程序并没有直接输出,采用与弯曲型相同的处理方式:模型对称布置,使质心在节点位置。
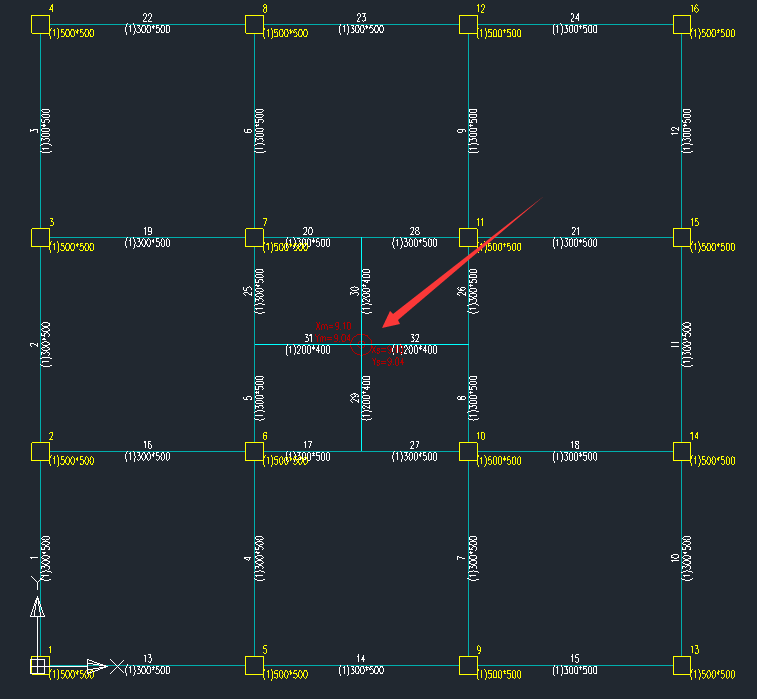
然后通过三维位移中的两点位移得到第4层质心的层间位移:
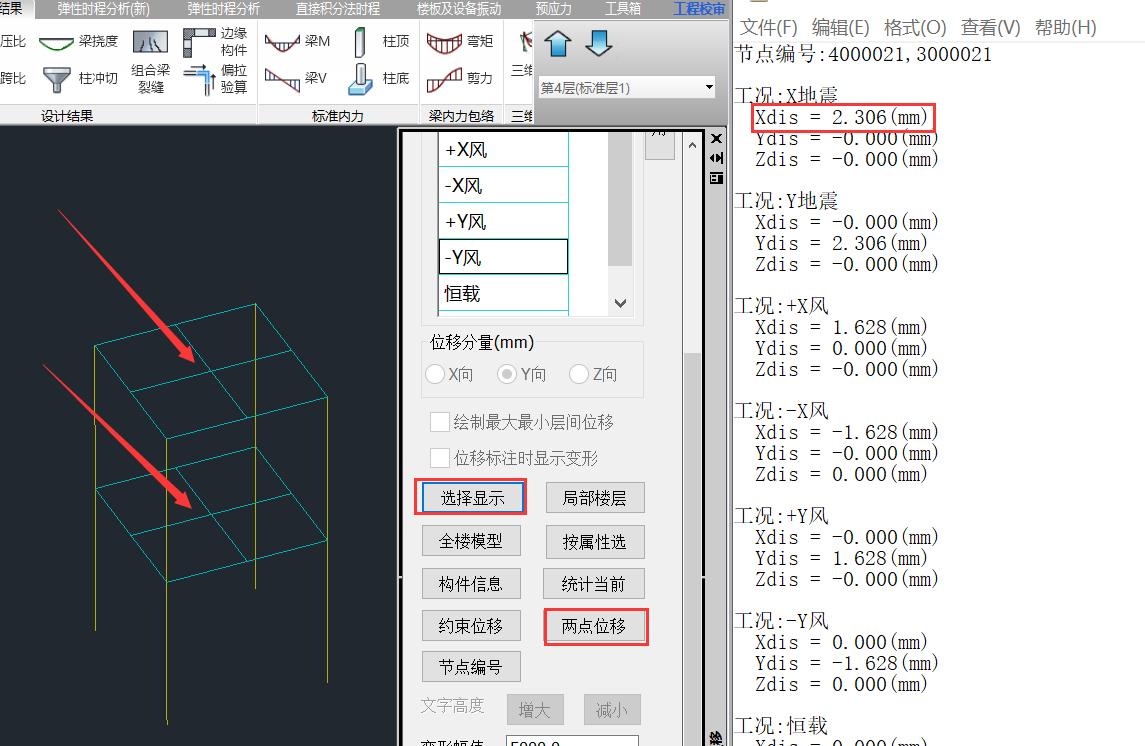
注:为了使读者看得更清楚模型采用了选择显示,只显示了中间一跨的构件。
则第4层的弹性等效侧向刚度:
D4=98.97/2.306x10-3=4.292x104kN/m

G4+ G5=2(1.2x3999+1.4x648)=11412kN
则刚重比:
D4xh4/(G4+G5)= 4.292x104x6/11412=22.565
和程序输出结果基本一致:
框架柱屈曲
对于结构稳定性,除了保证整体稳定之外,还应关注构件级别的稳定性。对于构件的失稳问题可以分为三类:分支点失稳(又称为平衡分岔失稳)、极值点失稳、跃越失稳。
分支点失稳是理想化的情况,即达到某种荷载时,除结构原来的平衡状态存在外,还可能出现第二个平衡状态,又称为平衡分岔失稳,在YJK 软件中的屈曲分析是解决线性屈曲问题,属于分支点失稳。
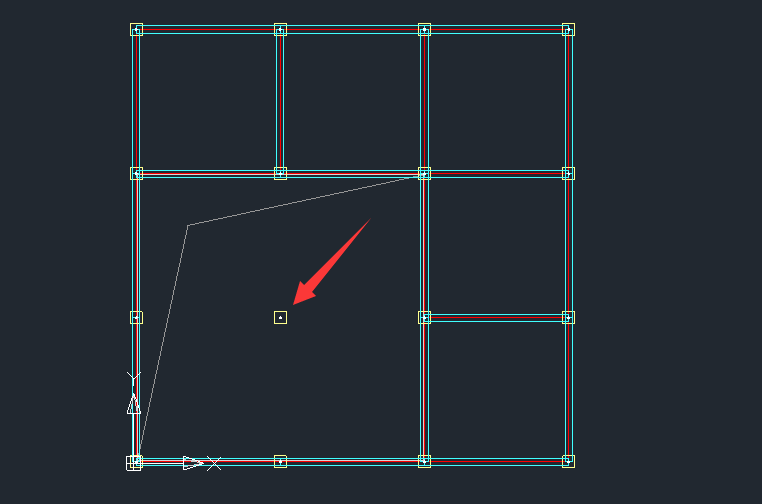
以下以一个示例模型用盈建科软件对跃层柱进行屈曲分析:
箭头处为1~4层跃层柱。
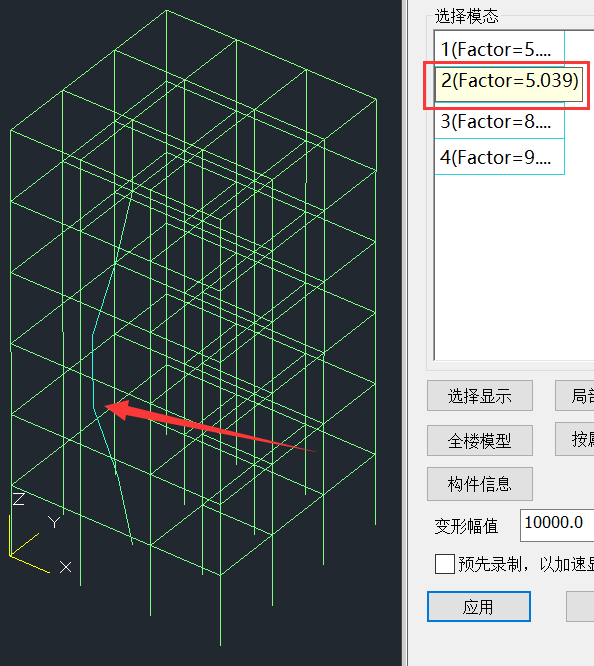
在变形图屈曲菜单下,第1、2阶分别为跃层柱沿2个方向弯曲变形占主导的模态(wmass.out文件也对应输出屈曲因子)。

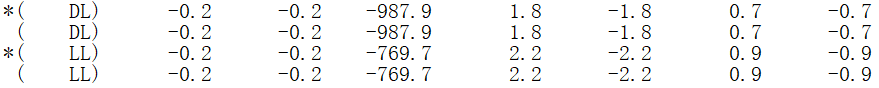
查看构件信息:
1.0恒+0.5活组合下跃层柱轴力为987.9+0.5*769.7=1372.75
则跃层柱的临界力:
Pcr=1372.75x5.038=6915.9kN
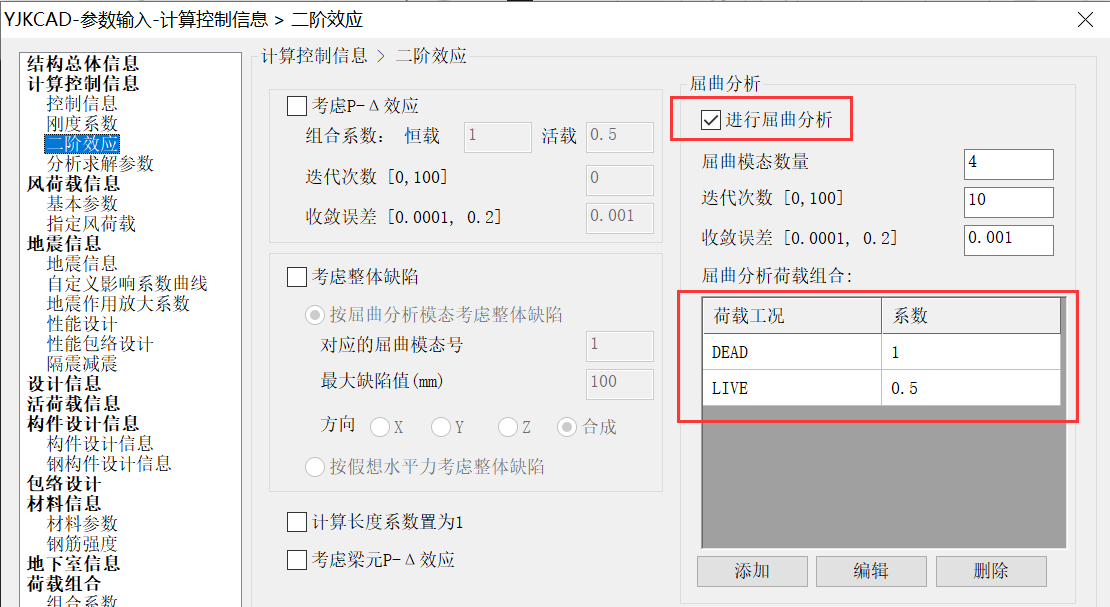
注:对于某些较刚的跃层柱,前几阶屈曲无法激发跃层柱的变形。则需要人为在分析柱上施加自定义荷载,然后进行自定荷载下的屈曲分析。
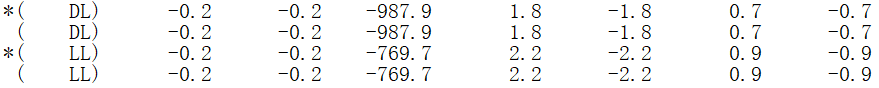
计算跃层柱的临界力和1.0恒+0.5活类似。
剪力墙稳定
当剪力墙截面较小或楼层层高较大时,剪力墙可能发生失稳破坏,《高规》附录D对剪力墙的稳定做了相关要求。
在实际工程中,T型、L型、槽型由于墙肢计算长度系数较小,基本不会出现稳定不满足的情况,较多情况是一字墙的稳定性不够。以某工程中的一字墙为例,进行剪力墙稳定性手核:
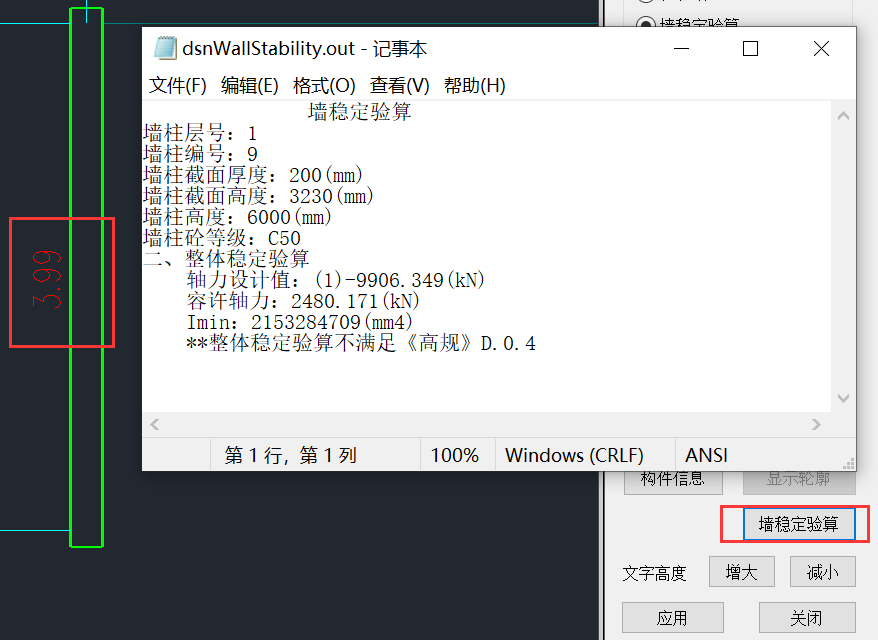
轴力设计值,可查看构件信息:

轴力设计值=1.3x(-6808.9)+1.5x(-703.2)=-9906.37kN
根据《高规》D.0.4

容许轴力=1.2x3.45x104x 2153284709/60002=2476277N=2476.28kN
稳定系数=9906.37/2476.28=4.0
手核结果和程序输出结果基本一致。